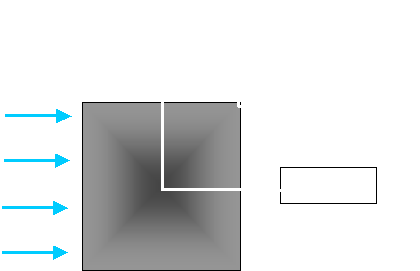
Example

Outline of building and approach wind characteristics

Building height H = 200 m

Building width B = 40 m

Building depth D = 40 m

Building natural frequency f_1x = 0.2 Hz, f_1y = 0.2 Hz, f_1z = 0.35 Hz

Average radius of gyration g = 18 m

Linear mode shape in all three directions

Damping ratio z= 0.02 (Composite Structural System)

Drag force coefficient C_D = 1.3

Building bulk density is 250 kg /m³

Air density r = 1.25 kg /m³

Location: an urban zone along Atlantic Coast of South Florida

According to ASCE7-98, this site is defined as Exposure A from all directions, with a = 1/3.0 (Table 6-4, ASCE 7-98)

Basic wind speed at reference height of 10 m in terms of 3-second gust, U₁₀ = 63 m/s (Fig. 6-1b, ASCE 7-98)

Note: The influences of wind direction, topography, shielding, importance factor, and return period are ignored in the discussion herein.

STEP 1. Computation of reduced frequency

The first step is to calculate the reduced frequency in terms of the mean wind speed at the building’s full height in Exposure Category A. This requires several conversions: (A) convert the wind speed at 10 m height in from a 3 second gust in open terrain to a wind speed with averaging time of 1 hour in Exposure A; (B) convert to full-height of the structure. Two scenarios are considered, the survivability design with a 50-year event for determination of base moments, and the serviceability design with a 10-year event for determination of RMS acceleration levels.

Survivability design (one-hour averaging time, 50-year return period)
Wind speed at 10 m height in terms of 3-second gust in open terrain = 63 m/s
A) Conversion to wind speed in terms of 1-hour mean in Exposure A = 63 ´ 0.30* = 18.9 m/s
B) Conversion to wind speed at 200 m height in terms of 1-hour mean in Exposure A = = 18.9 ´ (200/10)^1/3 = 51.30 m/s
= 0.156	= 0.156	= 0.273
Serviceability design (one-hour averaging time, 10-year return period)
Conversion to 3-second gust at 10 m height in open terrain for 10 year return period = 63 ´ 0.74** = 46.62 m/s
A) Conversion to 1-hour mean wind speed in Exposure A = 46.62 ´ 0.30* = 13.99 m/s
B) Conversion to wind speed at 200 m height in terms of 1-hour mean in Exposure A = = 13.99 ´ (200/10) ^1/3 = 37.96 m/s
= 0.211	= 0.211	= 0.369
*Conversion factor, , taken from Table 6-4 (ASCE 7-98) **Conversion factor shown in Table C6-3 (ASCE 7-98)

STEP 2. Access database for RMS moment coefficients and spectral values

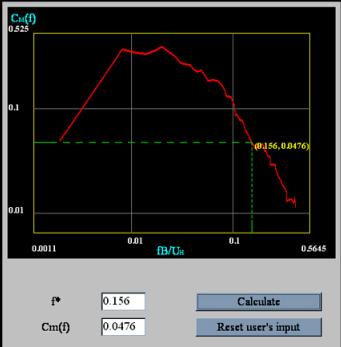
Using the Aerodynamic Loads Database for the case shown here, the values of the non-dimensionalized power spectrum and RMS coefficient can be identified. Note that these values have been rounded to three decimal places in this example. The accompanying snap shot illustrates this process for the alongwind survivability case.

		50-year	10-year	50-year	10-year
Alongwind	0.109	0.156	0.211	0.048	0.040
Acrosswind	0.133	0.156	0.211	0.192	0.073
Torsional	0.044	0.273	0.369	0.059	0.040

3. Look for RMS moment coefficients and spectral values from the database

STEP 3. Compute base moments and acceleration response

Using the values provided by the database, the background and resonant components of the base bending moment and base torque can be computed by Equations 11 and 12, as given in the procedure section of this website. The expression for the resonant peak factor is provided in the procedure, while the background peak factor can be assumed to be 3.4, in accordance with ASCE 7-98.

While the mean base moment for the acrosswind and torsional response is assumed zero, the alongwind mean base moment can be calculated by integrating the mean loads over the height:

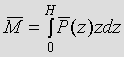
(13)

where the mean wind load per unit height is given by .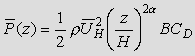

The peak base moment can then be determined in accordance with the combination rule (Eq. 7) in the procedure.

Survivability Design (50 year wind)

The values for the survivability design according the database are provided alongside the alongwind peak base moment determined from ASCE 7-98.

	Base moments (10^6 kN-m)
Alongwind by ASCE7-98	3.2790*	--	--	3.3117**
Alongwind	1.2831	0.9754	1.4915	3.0651
Acrosswind	0.0000	1.1902	3.6396	3.8293
Torsional	0.0000	0.0788	0.1386	0.1594
*Mean base moment, in 3-second averaging time. All other results in terms of 1-hour averaging time. , where the gust effect factor, G=1.01, as determined by Eq. 6-6 (ASCE 7-98). **Determined by net effect of pressures prescribed by Eq. 6-17 on windward and leeward faces, integrated over full height of structure.

Serviceability Design (10 year wind)

In the case of serviceability design for occupant comfort, RMS accelerations for a 10-year event become critical. Equation 8 in the procedure provided can be used to obtain peak accelerations, whose division by the resonant peak factor yields the RMS accelerations provided below. This requires the determination of the resonant component of the equivalent static wind loads given by Equations 5 & 6, in addition to the resonant base moments. In the case of the torsional component, the mass moment of inertia per unit height, I(z), is defined as m(z)g² where g is the radius of gyration.

The angular accelerations due to torsion may be separated into the resultant alongwind and acrosswind components at the corner of the structure, as shown by the accompanying figure. These lateral accelerations induced by torsion can be combined with those generated by sway motion to obtain the total lateral accelerations at the corner by the SRSS combination rule. Once again, ASCE 7-98 calculations for the alongwind accelerations are provided for comparison.

	RMS Accelerations at roof
Alongwind by ASCE 7-98	3.84 milli-g
Alongwind	3.76 milli-g
Acrosswind	6.20 milli-g
Lateral Accelerations at Corner Induced by Torsion	1.20´10^-3 rad/s^2	Alongwind component: 2.50 milli-g
		Acrosswind component: 2.50 milli-g
Total Lateral Accelerations at Corner	Alongwind component: 4.52 milli-g Acrosswind component: 6.69 milli-g

SUPPLEMENTAL INFORMATION: Wind Force Components

To illustrate the contributions of the background and resonant components in the various directions to the overall wind forces, the distribution of these wind force components along the building height are given in the plots and table below. While expressions for the resonant component of the equivalent static wind loads is provided by Equations 5 & 6 in the procedure, the methodology for the background component of these loads can be determined by expressions provided in Zhou and Kareem 2001. In this description, the wind loads are defined as point loads at each floor of the structure, assuming the floor-to-floor height to be 4 m.

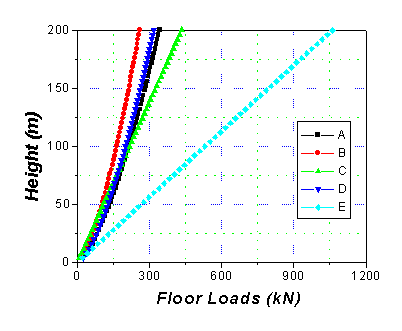
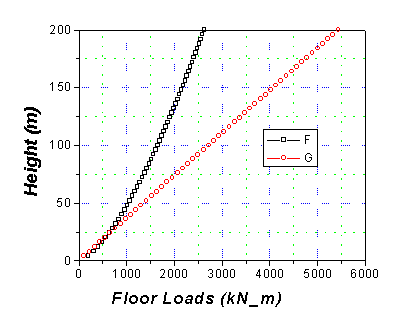
Table 1: Equivalent static wind loads

Height (m)	A	B	C	D	E	F	G
4	25.21	19.165	8.686	23.385	21.198	193.406	108.704
8	40.018	30.422	17.372	37.121	42.395	307.013	217.408
12	52.439	39.864	26.059	48.642	63.593	402.301	326.113
16	63.525	48.292	34.745	58.925	84.79	487.353	434.817
20	73.715	56.038	43.431	68.377	105.988	565.523	543.521
24	83.242	63.281	52.117	77.214	127.186	638.614	652.225
28	92.251	70.13	60.804	85.571	148.383	707.733	760.93
32	100.84	76.659	69.49	93.538	169.581	773.625	869.634
36	109.078	82.921	78.176	101.179	190.778	836.82	978.338
40	117.015	88.955	86.862	108.542	211.976	897.712	1087.042
44	124.691	94.791	95.549	115.662	233.173	956.604	1195.747
48	132.138	100.452	104.235	122.57	254.371	1013.736	1304.451
52	139.381	105.958	112.921	129.288	275.569	1069.3	1413.155
56	146.44	111.324	121.607	135.836	296.766	1123.456	1521.859
60	153.333	116.564	130.293	142.23	317.964	1176.336	1630.564
64	160.074	121.689	138.98	148.483	339.161	1228.053	1739.268
68	166.676	126.708	147.666	154.607	360.359	1278.704	1847.972
72	173.15	131.629	156.352	160.612	381.557	1328.37	1956.676
76	179.505	136.46	165.038	166.507	402.754	1377.124	2065.38
80	185.749	141.207	173.725	172.299	423.952	1425.03	2174.085
84	191.89	145.876	182.411	177.996	445.149	1472.143	2282.789
88	197.935	150.471	191.097	183.602	466.347	1518.515	2391.493
92	203.888	154.997	199.783	189.125	487.545	1564.189	2500.197
96	209.756	159.458	208.47	194.568	508.742	1609.205	2608.902
100	215.543	163.857	217.156	199.935	529.94	1653.601	2717.606
104	221.253	168.198	225.842	205.232	551.137	1697.408	2826.31
108	226.89	172.483	234.528	210.461	572.335	1740.657	2935.014
112	232.459	176.716	243.214	215.626	593.533	1783.375	3043.719
116	237.961	180.899	251.901	220.73	614.73	1825.587	3152.423
120	243.4	185.034	260.587	225.776	635.928	1867.317	3261.127
124	248.78	189.124	269.273	230.765	657.125	1908.586	3369.831
128	254.101	193.169	277.959	235.702	678.323	1949.413	3478.535
132	259.368	197.173	286.646	240.587	699.52	1989.817	3587.24
136	264.582	201.136	295.332	245.423	720.718	2029.815	3695.944
140	269.744	205.061	304.018	250.212	741.916	2069.423	3804.648
144	274.858	208.949	312.704	254.956	763.113	2108.655	3913.352
148	279.925	212.8	321.391	259.655	784.311	2147.526	4022.057
152	284.946	216.617	330.077	264.313	805.508	2186.048	4130.761
156	289.923	220.401	338.763	268.93	826.706	2224.233	4239.465
160	294.858	224.153	347.449	273.508	847.904	2262.094	4348.169
164	299.753	227.873	356.135	278.047	869.101	2299.64	4456.874
168	304.607	231.564	364.822	282.55	890.299	2336.882	4565.578
172	309.423	235.225	373.508	287.018	911.496	2373.83	4674.282
176	314.202	238.858	382.194	291.45	932.694	2410.492	4782.986
180	318.945	242.463	390.88	295.85	953.892	2446.878	4891.691
184	323.652	246.042	399.567	300.217	975.089	2482.995	5000.395
188	328.326	249.595	408.253	304.552	996.287	2518.851	5109.099
192	332.967	253.123	416.939	308.857	1017.484	2554.454	5217.803
196	337.576	256.627	425.625	313.132	1038.682	2589.811	5326.507
200	342.153	260.106	434.312	317.378	1059.879	2624.927	5435.212