Using the aerodynamic base bending moment or base torque as the input, the wind-induced response of a building can be computed using random vibration analysis by assuming idealized structural mode shapes, e.g. linear, and considering the special relationship between the aerodynamic moments and the generalized wind loads (e.g., Tschanz and Davenport 1983; Zhou et al. 2001). However, instead of utilizing conventional generalized wind loads, a base-bending-moment-based procedure is suggested for evaluating equivalent static wind loads and response, which is computationally more efficient, especially in cases where mode shape correction is required (Zhou et al. 2001). Application of this procedure for the alongwind response has proven effective in recasting the traditional gust loading factor approach in a new format (Zhou et al. 1999; Zhou and Kareem 2001a). The procedure can be conveniently adapted to the acrosswind and torsional response (Zhou and Kareem 2001b).

Assuming a stationary Gaussian process, the expected maximum base bending moment response in the alongwind or acrosswind directions or the base torque response can be expressed in the following form:

(1)

where and = expected extreme value and mean of the moment or torque response, respectively, g = peak factor, and s_M = root mean square (RMS) of the fluctuating base moment or base torque response, which can be computed by where S_M(f) = power spectral density (PSD) of the fluctuating base moment or torque response. It can be shown that the PSD of the moment response can be computed by the following equation (Zhou and Kareem 2001a):

(2)

where = structural transfer function of the first mode, f₁ and z₁ = natural frequency and critical damping ratio in the first mode, respectively, and S_M(f) = PSD of the aerodynamic base moment or torque. The flexibility to consider non-ideal mode shapes and non-uniform mass distributions has been addressed in (2) (Boggs and Peterka 1989; Zhou et al. 1999, 2001). Note that the same symbol, but expressed in bold, is employed here to distinguish the base moment or base torque response from the external aerodynamic moment or torque. The former includes the dynamic amplification effects due to wind fluctuations and structural dynamics.

To facilitate computations, the integration in (2) is divided into two portions, i.e., background and resonant components. The resonant base moment or base torque response, , can be computed in closed-form by assuming that the excitation can be represented by white-noise in the vicinity of the structure¡¯s natural frequency and by subsequently invoking the Residue Theorem for integration

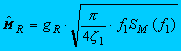
(3)

where = resonant peak factor, T = observation time, and subscript R = resonant component. The background base moment and base torque, , is equal to the aerodynamic quantity since, for the background response, the structure responds statically with a dynamic magnification factor of unity and

(4)

where g_B = background peak factor, which is usually at 3~4, s_M = RMS aerodynamic moment, and subscript B = background component. The mean base moment or base torque can be estimated from the HFBB test or by a mean pressure measurement test that is usually used as a companion test for the design of the cladding system.

Proceed to the next section

Notes :

See Complete List of Notations

See Publications Link for Complete Reference List.

If you have any questions or comments about the content of this site,
please e-mail to Dr. Ahsan Kareem, Dr. Tracy L. Kijewski-Correa or Dr. Dae-Kun Kwon