With the known base moment and base torque response, the equivalent static wind loading can be obtained by distributing the base moment to each floor in an appropriate manner as detailed in Zhou and Kareem (2001a, b). The equivalent static wind loads at height z for sway motions can be computed by

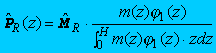
(5)

while for the torsional case,

(6)

where = resonant component of the equivalent static wind loading, m(z) = mass per unit height, I(z) = mass moment of inertia per unit height, and j₁(z) = fundamental mode shape in the direction of motion.

The wind-induced response, including the overall deflection, acceleration, internal forces, and stresses in each structural member can be computed using the equivalent static wind loads with a simple static analysis. For any response component, the resultant effect can be determined by summing the mean and the SRSS combination of the background and resonant components

(7)

where = resultant wind-induced response of interest, , , = mean, peak background and peak resonant response components, which are computed using the corresponding equivalent static wind load component with static analysis.

However, for the acceleration response, only the resonant component is of interest. For example, the peak acceleration in the sway mode can be computed by

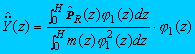
(8)

In the case of the torsional response, the mass per unit height, m(z), in (8) is replaced by I(z), the mass moment of inertia per unit height. The resulting RMS acceleration can then be determined by dividing the peak accelerations by the resonant peak factor, g_R.

Proceed to the example

Notes :

See Complete List of Notations

See Publications Link for Complete Reference List.

If you have any questions or comments about the content of this site,
please e-mail to Dr. Ahsan Kareem, Dr. Tracy L. Kijewski-Correa or Dr. Dae-Kun Kwon